Question

is (3,-3) a solution to the system 5x+4y=3, 2x-5y=19 need to be taught step by step please and thank you.

Answer 1

Basically all you’re doing is plugging in the inputs to the equations and see if they’re correct.

5(3)+4(-3)=3 this proves to be true
2(3)-5(-3)=21 not 19

Answer 2

(3,-3) is not a solution of the given system.

Solution:

The equations given in the problem are,

`5x+4y=3` ----- (i)

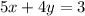`2x-5y=19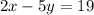` ------------ (ii)

Now if (3,-3) is a solution of the system then both equation will satisfy by substituting the value of x as 3 and y as -3. If any of the equation does not satisfy with (3,-3) then this is not the solution i.e. the given value should satisfy both the equations to be a solution.

So, now substituting value of (x, y) as (3,-3) on equation (i) we get

`5x+4y=3`

`5 *3 +4*(-3) = 3`

`15 -12 =3`

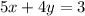
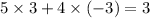
Here,
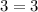`3=3` --- (a) (satisfies the first equation)

Again substituting value of (x, y) as (3,-3) on equation (ii) we get

`2x-5y=19`

`2*3-5*(-3) = 19`

`6+15 =19`

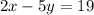
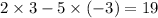
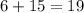
Here,
`21\\eq 19` --- (b) (does not satisfy the second equation)

From (a) and (b) we can conclude that the value (3.-3) does not satisfy the second equation. So, this is not a solution of the system.