Question

Find the sum of the geometric series with a1 = 243, r = -2/3, And n = 5

Answer 1

Sum of 5 terms of give geometric series is 165.

Solution:

Need to find the sum of geometric series.

Given that

First term of geometric series
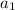`a_(1)` = 243

Common ratio of geometric series r =
`(-2)/(3)`

Number of terms in series = n = 5

Sum of geometric series when r < 1 is given by following formula

`s=(a_(1)\left(1-r^(n)\right))/(1-r)`
`(243\left(1-\left(-(2)/(3)\right)^(5))\right.)/(1-\left((-2)/(3)\right))`

`(243\left(1-\left((-32)/(243)\right)\right))/(1+(2)/(3))`

`((243(243+32))/(243))/((5)/(3))`

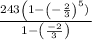
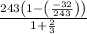
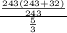
= 55 x 3 = 165

Hence sum of 5 terms of give geometric series is 165.