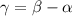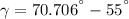Answer:
a)
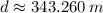 , b)
, b)
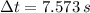 , c)
, c)

Step-by-step explanation:
a) The skier is experimenting an parabolic motion. The kinematic expressions for the skier are:
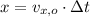
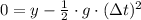
From trigonometry, there is the following relationship between vertical and horizontal components:
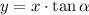
The following expression is constructed by substituting
 and
and
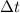 in the vertical motion expression and simplifying the resultant equation:
in the vertical motion expression and simplifying the resultant equation:
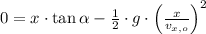
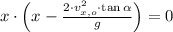
The roots of the second-order polynomial are:
 and
and
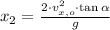
The second one represents the horizontal distance travelled by the skier:
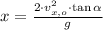
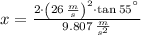
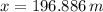
The vertical distance travelled by the skier is:
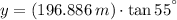

The distance that skier travels along the incline is computed through the Pythagorean Theorem:
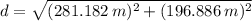
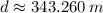
b) The time spent by the skier is:

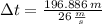
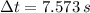
c) The final vertical velocity of the skier is:
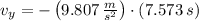

The absolute angle of the velocity is:

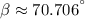
The magnitude of the relative angle with which the ski jumper hits the slope is: