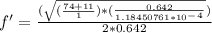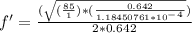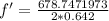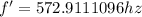Question

A guitar player can change the frequency of a string by "bending" it-pushing it along a fret that is perpendicular to its length. This stretches the string, increasing its tension and its frequency. The B string on a guitar is 64 cm long and has a tension of 74 N. The guitarist pushes this string down against a fret located at the center of the string, which gives it a frequency of 494 Hz. He then bends the string, pushing with a force of 4.0 N so that it moves 8.0 mm along the fret.

* What is the new frequency?

Answer 1

`f'=504hz`

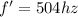
Step-by-step explanation:

From the question we are told that

The B string on a guitar is 64 cm long

The B string tension tension of 74 N.

Frequency of 494 Hz

Pushed with a Force of 4.0 N

It moves 8.0 mm along the fret.

Generally the equation for frequency of ring under tension is mathematically given as

`2Lf=\sqrt{x(T)/(\mu) }`

`2*(64/100)*494=\sqrt{(74)/(m/0.64)`

`(632.32)^2={(74)/(m/0.64)`

`(632.32)^2=74*{(0.64)/(m)`

`(632.32)^2={(47.36)/(m)`

`m=1.18450761*10^-^4`

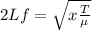
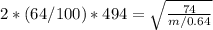
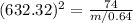
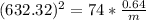
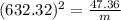
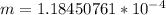
Therefore finding the New frequency f'

`f'=\frac{(\sqrt{(74+11)/(((1.18450761*10^-^4)/(0.642)))})}{2*0.642}`

`f'=\frac{(\sqrt{((74+11)/(1))*((0.642)/(1.18450761*10^-^4)})}{2*0.642}`

`f'=\frac{(\sqrt{((85)/(1))*((0.642)/(1.18450761*10^-^4)})}{2*0.642}`

`f'=\frac{(\sqrt{((54.57)/(1.18450761*10^-^4)})}{2*0.642}`

`f'=(678.7471973)/(2*0.642)`

`f'=572.9111096hz`