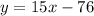Answer:
The quadratic function f(x)=15x-76
Solution:
As given in the problem, the two points are
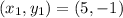 and
and
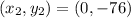
We know the slope
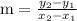
Now substituting the value of points we get,
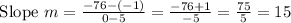
We know the equation of a line at a given point
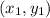 is
is
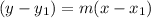
Let us take the point (5,-1) for the equation, then we get
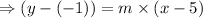
Multiplying the signs,
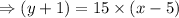
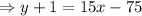
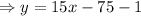
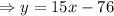
Hence, the function f(x) is