Question

A student that jumps a vertical height of 50 cm during the hang time activity.

a. What is the hang time of the student?
b. What speed must the student leave the ground with to reach that height?

Answer 1

The hang time of the student is 0.64 seconds, and he must leave the ground with a speed of 3.13 m/s

Why?

To solve the problem, we must consider the vertical height reached by the student as max height.

We can use the following equations to solve the problem:

Initial speed calculations:

`v_(f)^(2)=v_(o)^(2)+2*a*d`

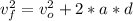
At max height, the speed tends to zero.

So, calculating, we have:

`v_(f)^(2)=v_(o)^(2)+2*a*d\\\\0=v_(o)^(2)+2*(-9.81(m)/(s^(2)))*0.5m\\\\v_(o)^(2)=9.81(m^(2) )/(s^(2))\\\\v_(o)=\sqrt{9.81(m^(2) )/(s^(2))}=3.13(m)/(s)`

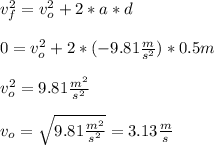
Hang time calculations:

We must remember that the total hang time is equal to the time going up plus the time going down, and both of them are equal,so, calculating the time going down, we have have:

`y-yo=vo.t+(1)/(2)*9.81(m)/(s^(2))*t^(2) \\\\0.5m-0=0*t+4.95*t^(2)\\\\t^(2)=(0.5)/(4.95)\\\\t=√(0.101)=0.318s`

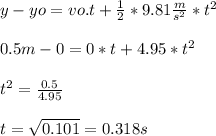
Then, for the total hang time, we have:

`TotalHangTime=2*0.318seconds=0.64seconds`

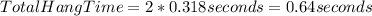
Have a nice day!