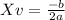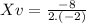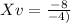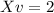Question

What is the equation of the axis of symmetry for the function shown below?

y+5=-2(x-2)^2


x=2 (done on apex)

Answer 1

x=2

Explanation:

Answer 2

x=2

Explanation:

The axis of symmetry can be calculated using the following formula:

`Xv= (-b)/(2a)`

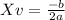
In order to use this formula, we need to have the function written in it's polynomial formula:

`f(x)=ax^(2) +bx+c`

In order to do so, we have to isolate Y from the excercise's formula.

`y=-2(x-2)^2-5`

Then we resolve the square of the binomial knowing that (a+b)^2=a^2+2.a.b+b^2

`(x-2)^2= x^2+2.x.(-2)+(-2)^2`

`(x-2)^2= x^2-4x+4`

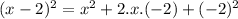
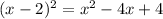
Now we have that:

`y=-2.(x^2-4x+4)-5`

`y=-2x^2+8x-8-5`

`y=-2x^2+8x-13`

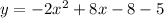
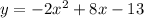
As we have now the polynomyal formula, we know that a=-2, b=8 and c=-13. We supplant on the formula and get:

`Xv= (-b)/(2a)`

`Xv= (-8)/(2.(-2))`

`Xv= (-8)/(-4))`

`Xv= 2`