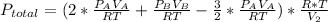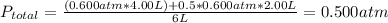Answer:
0.500 atm
Step-by-step explanation:
For the reaction
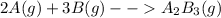
Assuming gas ideal
PV=nRT
P= pressure, V= volume of the container, n= mol of gas, R=constant of gases and T=temperature.
mol of A =
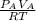
mol of B=
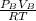
we don't know the temperature but we know that is constant so is the same in both flasks.
we need to know if one of the reagents is limiting the reaction or if they are in right proportions. When we see the expressions for the moles for each reagent we see that both have RT in the denominator and this value is constant so we can say that the number of moles of each reagent is proportional to just PiVi
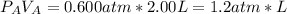
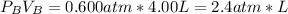
the stoichiometry relationship is:
3 mol of B need 2 mol of A
Applying the proportionality
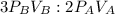
so 2.4 atm*L of B need
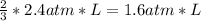 of A
of A
we just have 1.2atm*L of A so, this is the limiting reagent of the reaction.
Assuming theoretical yield we can say that all A was consumed and in the final condition we have the B that did not reacted and the product A2B3
The dalton's law tell us that the total pressure of a mixture of gases is the sum of the partial pressure of every gas.
So after the reaction the total pressure is:
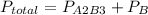
we can also say that the volume in the final condition is
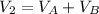
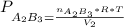
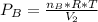
so P total is
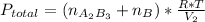
From the reaction stoichiometry we know that 2 mol of A produce 1 mol of
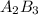
so
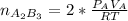
moles of B in the outlet would be

the moles of B used or consumed in the reaction are
mol of B = (3/2)A
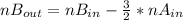
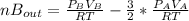
replacing
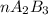 and nB in the total pressure equation we get:
and nB in the total pressure equation we get: