Question

Suppose you purchase a ten-year bond with 9% annual coupons. You hold the bond for four years and sell it immediately after receiving the fourth coupon. If the bond’s YTM was 8.66% when you purchased and sold the Bond. What cash flows will you pay at the purchase and what cash flows will you receive at the sale (including any coupon received immediately before sale) from you investment in the bond per $100 face value? How much interest income will you earn for holding this bond for four years in total?

Answer 1

Ans.

The cash flow that you paid at the purchase was $102.22

The cash flow that you received by selling it in year 4 (coupons and all) will be $137.54

The interest earned for holding it for 4 years is 8.66%

Step-by-step explanation:

Hi, first, we need to find the price of the bond, that is with the following equation.

`Price=(Coupon((1+YTM)^(n)-1) )/(YTM(1+YTM)^(n) ) +(FaceValue)/((1+YTM)^(n))`

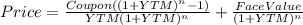
Where:

Coupon=100*0.09=9

YTM=0.0866

n = years to maturity, in our case, 10

So, what you pay for the bond is as follows.

`Price=(9((1+0.0866)^(10)-1) )/(0.0866(1+0.0866)^(10) ) +(100)/((1+0.0866)^(10) ) =102.22`

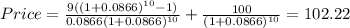
When you sell the bond, after receiving the 4th coupon, there is still 6 remaining coupons and the face value to be paid, so, the sell price in year 4 is:

`Price(4)=(9((1+0.0866)^(6)-1) )/(0.0866(1+0.0866)^(6) ) +(100)/((1+0.0866)^(6) ) =101.54`

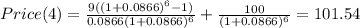
So the cash flow received by hold this bond for 4 years is:

`CashFlow=-Paid+Coupons+SellPrice`

`CashFlow=-102.22+36+101.54=35.33`

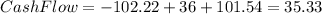
The right way to find the interest earned is by using the MS Excel function called, "IRR", but first you have to make a table in which you establish the right timing of receiving each cash flow, that should look like this.

Years Cash Flow

0 -$102,22

1 9

2 9

3 9

4 $110,54

IRR 8,66%

It is very important that you use the (-) sign in the beginning or the formula won´t work.

Besto of luck.