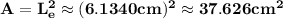Question

When a non-isotropic material is heated, the fractional increase in length is different along different directions. A rectangular plate with lengths l1 = 6.1 cm and l2 = 6.0 cm is made from such a material. In the direction along l1, the coefficient of linear expansion is α1 = 10 × 10−5 K−1 . In the direction of l2, the coefficient of linear expansion is α2 = 40 × 10−5 K−1 . The plate is heated until it becomes a perfect square. What is the area of the square?

Answer 1

The area of the square is
`\mathbf{37.626 cm^2}`

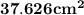
Step-by-step explanation:

The thermal linear expansion equation for each direction is given by

`L_1=l_1\left(1+\alpha_1\Delta T\right)\\L_2=l_2\left(1+\alpha_2\Delta T\right).`

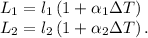
First, let's find the increase in temperature for which both lengths are equal

`L_e=L_1=L_2\\l_1\left(1+\alpha_1\Delta T\right)=l_2\left(1+\alpha_2\Delta T\right)\\l_1-l_2 = \left(l_2\alpha_2-l_1\alpha_1\right)\Delta T\\\Delta T = (l_1-l_2)/(l_2\alpha_2 - l_1\alpha_1),`

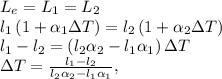
substituing the given values, we have

`\Delta T = (6.1cm - 6.0cm)/(6.0cm* 40* 10^(-5) K^(-1) - 6.1cm* 10* 10^(-5) K^(-1))\\\Delta T \approx 55.8659 K.`

Now, the area of the perfect square can be calculated from
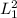`L_1^2` or
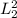`L_2^2` (at this temperature), indisctintly. Let's take the first one

`L_e = l_1\left(1+\alpha_1\Delta T\right)\\L_e = 6.1 cm\left(1+10* 10^(-5) K^(-1)* 55.8659 K\right)\\L_e \approx 6.1340 cm,`

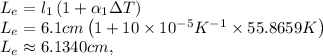
then

`\mathbf{A=L_e^2\approx (6.1340cm)^2 \approx 37.626cm^2}`