Answer:
Part (A) 16 cattle should be put on each diet in order to achieve a sufficiently small standard error.
Part (B) No, the required number of cattle should not double.
Explanation:
Consider the provided information.
The standard error of the mean for each diet should not exceed 5kg.
Therefore, sample mean is =

Part (A)
The population standard deviation of weight gain is guessed to be about 20kg on any of the diets,
From the above

It is given that

As we know

Thus,

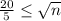


16 cattle should be put on each diet in order to achieve a sufficiently small standard error.
Part (B) If the guess of the s.d is doubled, to 40kg, does the required number of cattle double?
From the above
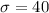
It is given that

Thus,
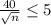
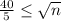


64 cattle are required, which is not the double of 16.
Hence, No, the required number of cattle should not double.