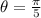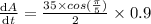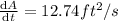Question

A triangle has two constant sides of length 5 feet and 7 feet. The angle between these two sides is increasing at a rate of 0.9 radians per second. Find the rate at which the area of the triangle is changing when the angle between the two sides is ????5.

Answer 1

Answer:
`12.74 ft^2/s`

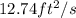
Explanation:

Given

Two sides of triangle of sides 5 ft and 7 ft

and angle between them is increasing at a rate of 0.9 radians per second

let
`\theta`is the angle between them thus

Area of triangle when two sides and angle between them is given

`A=(ab\sin C)/(2)`

`A=(5* 7* \sin \theta )/(2)`

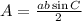
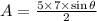
Differentiate w.r.t time

`\frac{\mathrm{d} A}{\mathrm{d} t}=(35\cos theta )/(2)* \frac{\mathrm{d} \theta }{\mathrm{d} t}`

at
`\theta =(\pi )/(5)`

`\frac{\mathrm{d} A}{\mathrm{d} t}=(35* cos((\pi )/(5)))/(2)* 0.9`

`\frac{\mathrm{d} A}{\mathrm{d} t}=12.74 ft^2/s`