Question

You are given three cubes, A, B, and C; one is magnesium, one is aluminum, and the third is silver. All three cubes have the same mass, but cube A has a volume of 25.9 mL, cube B has a volume of 16.7 mL, and cube C has a volume of 4.29 mL. Identify cubes A, B, and C.

Answer 1

The cube A is magnesium, the cube B is aluminum and the cube C is silver.

Step-by-step explanation:

Density is defined by the expression
`d=(m)/(V)` where m is the mass and V is the volume, therefore:

- Density of the cube A:

`d_(A)=(m_(A))/(V_(A))`

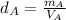
- Density of the cube B:

`d_(B)=(m_(B))/(V_(B))`

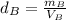
- Density of the cube C:

`d_(C)=(m_(C))/(V_(C))`

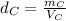
Solving for mass:

`m_(A)=d_(A)*V_(A)`

`m_(B)=d_(B)*V_(B)`

`m_(C)=d_(C)*V_(C)`

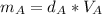
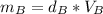
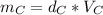
And all the three cubes have the same mass, so:

`m_(A)=m_(B)=m_(C)`

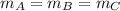
Therefore:

`d_(A)*V_(A)=d_(B)*V_(B)` (Eq.1)

`d_(A)*V_(A)=d_(C)*V_(C)` (Eq.2)

Solving for
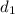`d_(1)` in Eq.1:

`d_(A)=d_(B)(V_(B))/(V_(A))`

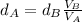
Replacing values for the volume:

`d_(A)=d_(B)(16.7mL)/(25.9mL)`

`d_(A)=d_(B)*0.64`

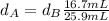
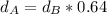
As we know the density of the aluminum is
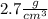`2.7(g)/(cm^(3))`, so replacing this value for
`d_(B)`:

`d_(A)=2.7(g)/(mL)*0.64`

`d_(A)=1.728(g)/(mL)`

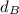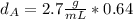
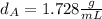
that is the density of the magnesium.

Solving for
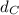`d_(C)` in Eq.2:

`d_(C)=d_(A)(V_(A))/(V_(C))`

`d_(C)=d_(A)(25.9mL)/(4.29mL)`

`d_(C)=d_(A)*6.04`

`d_(C)=1.728(g)/(mL)*6.04`

`d_(C)=10.4(g)/(mL)`

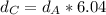
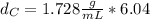
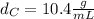
That is the density of the silver.

Therefore the cube A is magnesium, the cube B is aluminum and the cube C is silver.