Question

Find the slope of the line passing through the points (2, 7) and (-1, 4).

1. -1
2. 1
3. 3

Answer 1

`\bf (\stackrel{x_1}{2}~,~\stackrel{y_1}{7})\qquad (\stackrel{x_2}{-1}~,~\stackrel{y_2}{4}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{4}-\stackrel{y1}{7}}}{\underset{run} {\underset{x_2}{-1}-\underset{x_1}{2}}}\implies \cfrac{-3}{-3}\implies 1`

Answer 2

Option 2

ANSWER:

The slope of the line passing through the points (2, 7) and (-1, 4) is 1

SOLUTION:

Given, two points are (2, 7) and (-1, 4).

We need to find the slope of a line which passes through the given two points.

Now, we know that, slope of a line which passes through the points
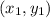`(x_(1) , y_(1))` and
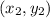`(x_(2) , y_(2))` is given by

`\mathrm{m}=(y_(2)-y_(1))/(x_(2)-x_(1))`

`\text { Here, in our problem, } x_(1)=-1, y_(1)=4 \text { and } x_(2)=2, y_(2)=7`

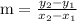
Now, substitute the above values in slope formula.

`\begin{aligned} m &=(7-4)/(2-(-1)) \\=& (7-4)/(2+1)=(3)/(3) \end{aligned}`

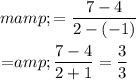
Slope “m” = 1

Hence, the slope of the required line is 1.