Question

(43 points) In the US, 85% of the population has Rh positive blood. Suppose we take a random sample of 6 persons and let Y denote the number of persons, out of 6, with Rh positive blood. a. (7 points) What is the distribution of Y ? Please name the distribution and provide the parameter values for the distribution. b. (10 points) What is the probability that Y is less than 6? c. (20 points) Suppose 200 persons are randomly selected from the US population. What is the approximate probability that there are fewer than 160 persons with Rh positive blood in a sample of 200? d. (6 points) State the large sample assumptions needed in (c).

Answer 1

Answer:

a) Binomial distribution with parameters p=0.85 q=0.15 n=6

b) 62.29%

c) 2.38%

d) See explanation below

Explanation:

a)

We could model this situation with a binomial distribution

`P(6;k)=\binom{6}{k}p^kq^(6-k)`

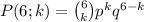
where P(6;k) is the probability of finding exactly k people out of 6 with Rh positive, p is the probability of finding one person with Rh positive and q=(1-p) the probability of finding a person with no Rh.

So

`\bf P(Y=k)=\binom{6}{k}(0.85)^k(0.15)^(6-k)`

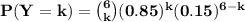
b)

The probability that Y is less than 6 is

P(Y=0)+P(Y=1)+...+P(Y=5)

Let's compute each of these terms

`P(Y=0)=P(6;0)=\binom{6}{0}(0.85)^0(0.15)^(6)=1.139*10^(-5)`

`P(Y=1)=P(6;1)=\binom{6}{1}(0.85)^1(0.15)^(5)=0.0000387281`

`P(Y=2)=P(6;2)=\binom{6}{2}(0.85)^2(0.15)^(4)=0.005486484`

`P(Y=3)=P(6;3)=\binom{6}{3}(0.85)^3(0.15)^(3)=0.041453438`

`P(Y=4)=P(6;4)=\binom{6}{4}(0.85)^4(0.15)^(2)=0.176177109`

`P(Y=5)=P(6;5)=\binom{6}{5}(0.85)^5(0.15)^(1)=0.399334781`

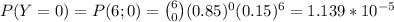
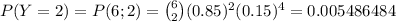
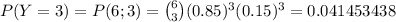
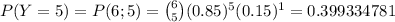
and adding up these values we have that the probability that Y is less than 6 is

`\sum_(i=1)^(5)P(Y=i)=0.622850484\approx 0.6229=62.29\%`

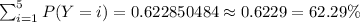
c)

In this case is a binomial distribution with n=200 instead of 6.

p and q remain the same.

The mean of this sample would be 85% of 200 = 170.

In a binomial distribution, the standard deviation is

`s = √(npq)`

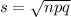
In this case

`√(200(0.85)(0.15))=5.05`

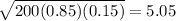
Let's approximate the distribution with a normal distribution with mean 170 and standard deviation 5.05

So, the approximate probability that there are fewer than 160 persons with Rh positive blood in a sample of 200 would be the area under the normal curve to the left of 160

(see picture attached)

We can compute that area with a computer and find it is

0.0238 or 2.38%

d) In order to approximate a binomial distribution with a normal distribution we need a large sample like the one taken in c).

In general, we can do this if the sample of size n the following inequalities hold:

`np\geq 5 \;and\;nq \geq 5`

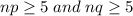
in our case np = 200*0.85 = 170 and nq = 200*0.15 = 30