Answer :
The first term of a sequence is -87. 165 is 37th term of given Arithmetic sequence.
Solution:
Given that ;
First term of the sequence
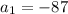
Also each successive term is created by adding 7 to its previous term. This means given sequence is an arithmetic sequence with common difference d = 7.
Let’s say 165 be
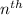 term of above arithmetic sequence that is
term of above arithmetic sequence that is
 = 165. We need to determine n.
= 165. We need to determine n.
Formula of
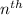 term of arithmetic sequence is as follows:
term of arithmetic sequence is as follows:
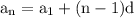
where
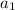 is the first term of the sequence
is the first term of the sequence
"d" is the common difference ratio
Substituting the given values we get
165 = -87 + (n-1) 7
165 + 87 = 7n – 7
7n = 165 + 87 + 7
n =
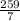 = 37
= 37
Hence 165 is 37th term of given Arithmetic sequence.