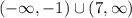Answer:
The function
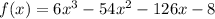 is decreasing on the interval
is decreasing on the interval
 and it is increasing on the interval
and it is increasing on the interval
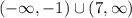
Explanation:
To determine the intervals of increase and decrease of the function
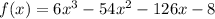 , perform the following steps:
, perform the following steps:
1. Differentiate the function
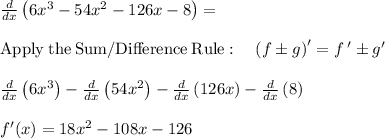
2. Obtain the roots of the derivative, f'(x) = 0

3. Form open intervals with the roots of the derivative and take a value from every interval and find the sign they have in the derivative.
If f'(x) > 0, f(x) is increasing.
If f'(x) < 0, f(x) is decreasing.
On the interval
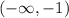 , take x = -2,
, take x = -2,
 f'(x) > 0 therefore f(x) is increasing
f'(x) > 0 therefore f(x) is increasing
On the interval
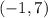 , take x = 0,
, take x = 0,
 f'(x) < 0 therefore f(x) is decreasing
f'(x) < 0 therefore f(x) is decreasing
On the interval
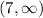 , take x = 10,
, take x = 10,
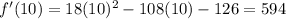 f'(x) > 0 therefore f(x) is increasing
f'(x) > 0 therefore f(x) is increasing
The function
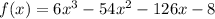 is decreasing on the interval
is decreasing on the interval
 and it is increasing on the interval
and it is increasing on the interval