Question

Be sure to answer all parts. Liquid nitrogen trichloride is heated in a 3.00−L closed reaction vessel until it decomposes completely to gaseous elements. The resulting mixture exerts a pressure of 839 mmHg at 86°C. What is the partial pressure of each gas in the container?

Answer 1

`p_(Cl_2)=629.25mmHg\\p_(N_2)=209.75mmHg`

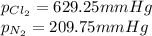
Step-by-step explanation:

Hello,

At first, consider the chemical reaction:

`2NCl_3-->3Cl_2+N_2`

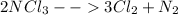
Now, considering the ideal gas equation, we compute the total moles:

`PV=nRT\\n=(PV)/(RT) \\n=(839mmHg*(1atm)/(760mmHg)*3L )/(0.082(atm*L)/(mol*K)*359K )\\ n=0.1125mol`

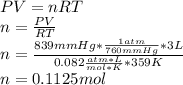
Then, taking into account that the total moles are stoichiometrically handed out by the half (0.05625mol), one can say that:

`n_(Cl_2)=0.05625molNCl_3*(3mol Cl_2)/(2molNCl_3) =0.084375molCl_2\\n_(N_2)=0.05625molNCl_3*(1mol N_2)/(2molNCl_3) =0.028125molN_2`

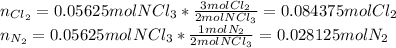
Thus, the molar fractions are:

`x_(Cl_2)=(0.084375)/(0.1125) =0.75\\x_(N_2)=(0.028125)/(0.1125) =0.25`

Finally, the partial pressures are:

`p_(Cl_2)=x_(Cl_2)P=0.75*839mmHg=629.25mmHg\\p_(N_2)=x_(N_2)P=0.25*839mmHg=209.75mmHg`

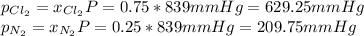
Best regards.