Answers:
a) 0.091
Step-by-step explanation:
We are given the following information in the question:
Mean, μ = 140 minutes
Standard Deviation, σ = 15 minutes
We are given that the distribution of time watching videos is a bell shaped distribution that is a normal distribution.
Formula:
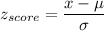
a) P(time is less than 120 minutes)

Calculating the value from the standard normal table we have,

The probability that an 18- to 24-year-old spends less than 120 minutes watching video on his or her smartphone per month is 0.091