Question

Find the value of r in (4,r),(r,2) so that the slope of the line containing them is -5/3

Answer 1

The value of r in (4,r),(r,2) so that the slope of the line containing them is
`(-5)/(3)` is 7

Solution:

Slope of the line which is passes through
`\left(\mathrm{x}_(1), \mathrm{y}_(1)\right) \text { and }\left(\mathrm{x}_(2), \mathrm{y}_(2)\right) \text { is }`

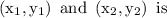
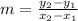`m=(y_(2)-y_(1))/(x_(2)-x_(1))` → (1)

From question given that two points are (4, r), (r, 2). Hence we get
`x_(1)=4 ; x_(2)=r ; y_(1)=r ; y_(2)=2`

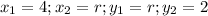
By substituting the values in equation (1),

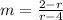`m=(2-r)/(r-4)` → (2)

Also given that slope that is m =
`(-5)/(3)`, so on substituting the value of m in equation (2),

`-(5)/(3)=(2-r)/(r-4)`

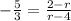
On simplifying,

-5r+20=6-3r

5r-3r=20-6

2r = 14

r =7

Hence value of r is 7.