Answer:
We first to know that if the wheel rotates from rest means that at t=0 the velocity and the angle rotated is 0.
Then, we know:
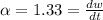
Integrating 2 times, we have:
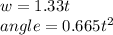
For the first 27.9 s, we have:
w = 37.107 rad/s
angle = 517.6426 rad
For the next seconds, according to the text, the angular velocity is constant so
w = 37.107 rad/s and hence, integrating:
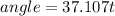
Then, the time remaining is:
53.5 - 27.9 = 25.6
So for the next 25.6 seconds we have:
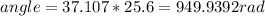
Finally, we add the 2 angles and we have as a result:
