Question

1. [5 pts] A rectangular swimming pool measures 14 feet by 30 feet. The pool is surrounded on all four sides by a path that is 3 feet wide. If the cost to resurface the path is $2 per square foot, what is the total cost of resurfacing the path? 2. The Great Pyramid outside Cairo, Egypt, has a square base measuring 756 feet on a side and a height of 480 feet. a. [3 pts] What is the volume of the Great Pyramid, in cubic yards? b. [2 pts] The stones used to build the Great Pyramid were limestone blocks with an average volume of 1.5 cubic yards. Assuming a solid pyramid, how many of these blocks were needed to construct the Great Pyramid?

Answer 1

1) $600

2) a) 3386880 cubic yards

b) 2257920 limestone

Explanation:

1)

Given;

Dimensions of the swimming pool = 14 feet × 30 feet

Dimensions of the pool with 3 feet wide path = ( 14 + 2 × 3 ) feet × ( 30 + 2 × 3 ) feet

= 20 feet × 36 feet

[ 2 × width of path is added because the width is to be added both the sides i.e 3 + 3 = 2 × 3 ]

Now,

The area without the path = 14 feet × 30 feet = 420 ft²

The area with the path = 20 feet × 36 feet = 720 ft²

Therefore,

the area of the path = 720 ft² - 420 ft² = 300 ft²

also,

cost to resurface = $2 per square feet

therefore,

The total cost to resurface = $2 × 300 = $600

2) Sides of the base of the pyramid = 756 feet

height of the pyramid = 480 feet

also,

1 feet =
`(1)/(3)` yards

thus,

Sides of the base of the pyramid =
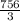`(756)/(3)` yards = 252 yards

height of the pyramid =
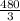`(480)/(3)` yards = 160 yards

therefore,

the volume of the pyramid =
`\frac{\textup{1}}{\textup{3}}*\textup{area of the base}*\textup{height}`

=
`\frac{\textup{1}}{\textup{3}}*\textup{252}^2*\textup{160}`

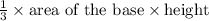
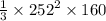
= 3386880 cubic yards

b) average volume of limestone 1.5 cubic yards

Therefore,

The number of stones required =
`\frac{\textup{Volume of pyramid}}{\textup{volume of stone}}`

=
`\frac{\textup{3386880}}{\textup{1.5}}`

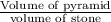
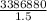
= 2257920 limestone