Answer:
a)Amplitude ,A = 2 mm
b)f=95.49 Hz
c)V= 30 m/s ( + x direction )
d) λ = 0.31 m
e)Umax= 1.2 m/s
Step-by-step explanation:
Given that
![y=2\ mm\ sin[(20m^(-1))x-(600s^(-1))t]](https://img.qammunity.org/2020/formulas/physics/high-school/qzbxvu9g6spt41l3c8wa1oasejd5ljgaqo.png)
As we know that standard form of wave equation given as

A= Amplitude
ω=Frequency (rad /s)
t=Time
Φ = Phase difference
![y=2\ mm\ sin[(20m^(-1))x-(600s^(-1))t]](https://img.qammunity.org/2020/formulas/physics/high-school/qzbxvu9g6spt41l3c8wa1oasejd5ljgaqo.png)
So from above equation we can say that
Amplitude ,A = 2 mm
Frequency ,ω= 600 rad/s (2πf=ω)
ω= 2πf
f= ω /2π
f= 300/π = 95.49 Hz
K= 20 rad/m
So velocity,V
V= ω /K
V= 600 /20 = 30 m/s ( + x direction )
V = f λ
30 = 95.49 x λ
λ = 0.31 m
We know that speed is the rate of displacement
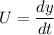
![U=2\ mm\ sin[(20m^(-1))x-(600s^(-1))t]](https://img.qammunity.org/2020/formulas/physics/high-school/nk308iya4hxfurnjfwis6zsppv9apqblrn.png)
![U=1200\ cos[(20m^(-1))x-(600s^(-1))t]\ mm/s](https://img.qammunity.org/2020/formulas/physics/high-school/zu8b72gbbue93yqqvc38j7xus225r454d3.png)
The maximum velocity
Umax = 1200 mm/s
Umax= 1.2 m/s