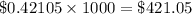Question

In the game of​ roulette, a player can place a ​$88 bet on the number 3232 and have a StartFraction 1 Over 38 EndFraction 1 38 probability of winning. If the metal ball lands on 3232​, the player gets to keep the ​$88 paid to play the game and the player is awarded an additional ​$280280. ​ Otherwise, the player is awarded nothing and the casino takes the​ player's ​$88. What is the expected value of the game to the​ player? If you played the game 1000​ times, how much would you expect to​ lose?

Answer 1

The expected value of the game to the player is
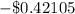`-\$0.42105`. A loss of $0.42105 is expected.

If you played the game 1000​ times, the amount that you are expected to lose is
`\$421.05`

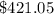
Explanation:

From the information given we know:

• The probability of winning is
  `(1)/(38)`
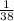
• If the player wins, he gets to keep the ​$8 paid to play the game and the player is awarded an additional ​$280.
• If the player loses, the casino takes the​ player's ​$8

There are 38 slots on a roulette wheel so the probability of losing is
`(37)/(38)`

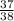
We can find an expected value by multiplying each numerical outcome by the probability of that outcome and then summing those products together.

The expected value in dollars for this game is

`(\$280\cdot (1)/(38))-(\$8 \cdot (37)/(38) )=-(8)/(19)\approx\$-0.42105`

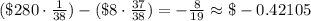
A loss of $0.42105 is expected.

If you played the game 1000​ times, the amount that you are expected to lose is
`\$0.42105 * 1000=\$421.05`