Question

Consider two copper wires with the same cross-sectional area. Wire A is twice as long as wire B. How do the resistivities and resistances of the two wires compare?

Check all that apply.
A. Wire B has twice the resistance of wire A. Wire B has twice the resistivity of wire A.
B. Wire A has twice the resistance of wire B. Wire A and wire B have the same resistivity.
C. Wire A and wire B have the same resistance.
D. Wire A has twice the resistivity of wire B.

Answer 1

Wire A has wire resistance as wire B and both wire have resistivity

So option is B is correct answer

Step-by-step explanation:

We have given that wire A has twice the length as of wire B
`l_A=2l_B`

And area of cross section is same so
`A_a=A_b`

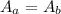
We know that resistance is given by
`R=(\rho l)/(A)`

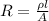
So
`R_a=(\rho l_a)/(A_a)` and
`R_b=(\rho l_b)/(A_b)`

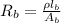
From the resistance expression we can see that resistance is directly proportional to length

As
`l_A=2l_B`

So resistance of wire A is twice the resistance of wire B

And as both the wire is made up of copper so resitivity will be same

So option B will be correct option