Question

1. Refer to the equation 3x − 4y = 12. (a) Create a table of values for at least 4 points. Show your work on how you found the values for each coordinate pair, and validated the points were on the line.

Answer 1

The table of values is attached.

The graph of the line shows that the points
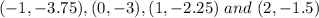`(-1,-3.75), (0,-3), (1, -2.25)\ and\ (2,-1.5)` lie on the line.

Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Given the equation:

`3x-4y = 12`

We can solve for the variable "y" in order to write in Slope-Intercept form:

`3x-4y = 12\\\\-4y=-3x+12\\\\y=(3)/(4)x-3`

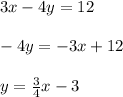
The nex step is to give values to the variables "x", then substitute each value into the equation and evaluate, in order to find the correspondings values of "y".

`For\=-1:\\\\y=(3)/(4)(-1)-3=-3.75`

`For\ x=0:\\\\y=(3)/(4)(0)-3=-3`

`For\ x=1:\\\\y=(3)/(4)(1)-3=-2.25`

`For\ x=2:\\\\y=(3)/(4)(2)-3=-1.5`

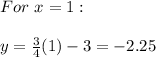
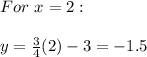
With this values we can make the table attached.

We can identify the slope of the line and the y-intercept are:

`m=(3)/(4)\\\\b=-3`

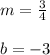
Then we can graph it

Observe that the points
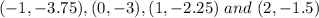`(-1,-3.75), (0,-3), (1, -2.25)\ and\ (2,-1.5)` lie on the line.