Question

A motorcycle has a constant speed of 22.7 m/s as it passes over the top of a hill whose radius of curvature is 179 m. The mass of the motorcycle and driver is 342 kg. Find the magnitude of (a) the centripetal force and (b) the normal force that acts on the cycle.

Answer 1

On the hill, (a) the centripetal force is
`\mathbf{932.70N}`, approximately and on the top of the hill, (b) the normal force exerted on the cycle is
`\mathbf{4411.14N}`.

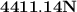Step-by-step explanation:

In this case, uniform circular movement equations are suitable, then (a) the centripetal force is given by

`F_c=(mv^2)/(r)=(324kg*\left(22.7(m)/(s)\right)^2)/(179m) \approx \mathbf{932.70N}.`

Now, (b) at the top of the fill, where weight alligns with the centripetal force and the normal, by applying Newton's second law, we have

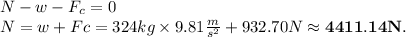`N-w-F_c=0\\N=w+Fc=324kg* 9.81(m)/(s^2)+932.70N \approx \mathbf{4411.14N}.`.