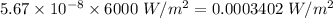Question

The sun as a blackbody:

a. The Sun is a 6000-K blackbody. At what characteristic wavelength does it radiate?

b. At what characteristic wavelength does a blackbody at room temperature radiate?

c. How much power per unit area is the Sun radiating?

Answer 1

Step-by-step explanation:

(a) Using Wien's displacement law which states that the temperature and the wavelength of the blackbody radiation are inversely proportional.

So,

λmax= b/T

Where,

λmax is the peak of wavelength

b is the Wien's displacement constant having value as
`2.9* 10^(-3)\  m K`

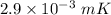
T is the Absolute Temperature in Kelvins = 6000 K

So,

λmax= b/T =
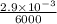`(2.9* 10^(-3))/(6000)` = 4.8333 × 10⁻⁷ m

It lies in the visible region.

(b) Using Wien's displacement law:

λmax= b/T

So,

λmax= b/T =
`(2.9* 10^(-3))/(298)` = 9.73154 × 10⁻⁶ m

This wavelength corresponds to infrared region.

(c) The expression for power per unit area by using Stefan–Boltzmann law is:

Power per unit area = εσT⁴

Where, ε = 1 for blackbody

σ is Stefan–Boltzmann constant, having value as
`5.67* 10^(-8)\ W/m^2K^4`

Thus,

P =
`5.67* 10^(-8)* 6000\ W/m^2=0.0003402\ W/m^2`