Question

The mean yearly rainfall in Sydney, Australia, is about 137 mm and the standard deviation is about 69 mm ("Annual maximums of," 2013). Assume rainfall is normally distributed. a.) State the random variable. b.) Find the probability that the yearly rainfall is less than 100 mm. c.) Find the probability that the yearly rainfall is more than 240 mm. d.) Find the probability that the yearly rainfall is between 140 and 250 mm. e.) If a year has a rainfall less than 100mm, does that mean it is an unusually dry year? Why or why not? f.) What rainfall amount are 90% of all yearly rainfalls more than?

Answer 1

a) The random variable is the mean yearly rainfall in Sydney, Australia.

b) There is a 29.46% probability that the yearly rainfall is less than 100 mm.

c) There is a 6.81% probability that the yearly rainfall is more than 240mm.

d) There is a 43.35% probability that the yearly rainfall is more than 240 mm.

e) Since the probability of a year having a rainfall of less than 100mm is 29.46%, as we found in b), it would not be an unusually dry year.

f) 90% of all yearly rainfalls are more than 48.335mm.

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by

`Z = (X - \mu)/(\sigma)`

After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X. Subtracting 1 by the pvalue, we This p-value is the probability that the value of the measure is greater than X.

In this problem, we have that:

The mean yearly rainfall in Sydney, Australia, is about 137 mm and the standard deviation is about 69 mm, so
`\mu = 137, \sigma = 69`.

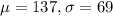a.) State the random variable.

The random variable is the mean yearly rainfall in Sydney, Australia.

b.) Find the probability that the yearly rainfall is less than 100 mm.

This is the pvalue of Z when
`X = 100`.

`Z = (X - \mu)/(\sigma)`

`Z = (100 - 137)/(69)`

`Z = -0.54`

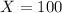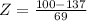
`Z = -0.54` has a pvalue of 0.2946.

This means that there is a 29.46% probability that the yearly rainfall is less than 100 mm.

c.) Find the probability that the yearly rainfall is more than 240 mm.

This is 1 subtracted by the pvalue of Z when
`X = 240`.

`Z = (X - \mu)/(\sigma)`

`Z = (240 - 137)/(69)`

`Z = 1.49`

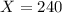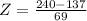
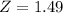
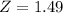`Z = 1.49` has a pvalue of 0.9319.

So, there is a 1-0.9319 = 0.0681 = 6.81% probability that the yearly rainfall is more than 240mm.

d.) Find the probability that the yearly rainfall is between 140 and 250 mm.

This is the pvalue of Z when
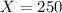`X = 250` subtracted by the pvalue of Z when
`X = 140`.

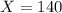For X = 250

`Z = (X - \mu)/(\sigma)`

`Z = (250 - 137)/(69)`

`Z = 1.64`

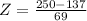
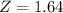
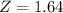`Z = 1.64` has a pvalue of 0.9495

For X = 140

`Z = (X - \mu)/(\sigma)`

`Z = (140 - 137)/(69)`

`Z = 0.04`

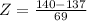
`Z = 0.04` has a pvalue of 0.5160.

So, there is a 0.9495 - 0.5160 = 0.4335 = 43.35% probability that the yearly rainfall is more than 240 mm.

e.) If a year has a rainfall less than 100mm, does that mean it is an unusually dry year? Why or why not?

A probability is unusually low when there is a lesser than 5% of it happening.

Since the probability of a year having a rainfall of less than 100mm is 29.46%, as we found in b), it would not be an unusually dry year.

f.) What rainfall amount are 90% of all yearly rainfalls more than?

This rainfall is the 10th percentile of rainfall.

The first step is to find Z that has a pvalue of 0.10. This is between
`Z = -1.28` and
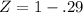`Z = 1-.29`. So this aount of rainfall is X when
`Z = -1.285`

`Z = (X - \mu)/(\sigma)`

`-1.285 = (X - 137)/(69)`

`X - 137 = -88.665`

`X = 48.335`

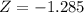
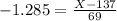
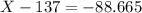
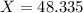
90% of all yearly rainfalls are more than 48.335mm.