Answer:
(a)
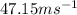
(b)
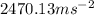
(c) 1235.06N and 252.05 as a ratio
Step-by-step explanation:
From Newton's second law of motion
F=ma where m is mass, a is acceleration and F is net force
Also from kinetic equation of motion, velocity and displacement are related using equation
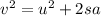
Where v is final velocity, u is initial velocity, a is acceleration and s is displacement
From the free body diagram attached, final velocity at maximum height is 0 and initial velocity is
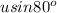
Also, the vertical component can be written as
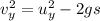 The negative sign before 2gs means displacement is opposite the gravitational force
The negative sign before 2gs means displacement is opposite the gravitational force
Where g is acceleration due to gravity,
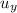 is vertical component of initial velocity and
is vertical component of initial velocity and
 is vertical component of final velocity
is vertical component of final velocity
Since
 is 0
is 0
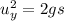
s=110 and g is taken as 9.8
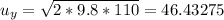
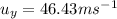
Also, it's evident that the vertical component of initial velocity is
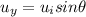 where
where
 is angle of projection and
is angle of projection and
 is resultant velocity
is resultant velocity
Making
 the subject we obtain
the subject we obtain
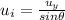
Since
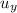 and
and
 are known as
are known as
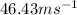 and
and
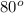 respectively, then
respectively, then

Therefore, the velocity of potato is
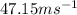
(b)
Displacement depends on length of tube hence s=0.450m hence going back to kinetic equation
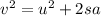
The final velocity v is answer in part a which is
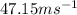 , initial velocity u is
, initial velocity u is
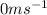 hence the equation is re-written as
hence the equation is re-written as
 and making a the subject we obtain
and making a the subject we obtain
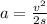
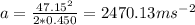
Therefore, average acceleration is
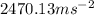
(c)
From Newton's second law of motion, F=ma where m=0.500kg and a is
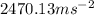
Therefore, the average force of potato is
F=0.5*2470.13=1235.06N
F=1235.06N
The weight, W of potato is given by W=mg
Taking R as ratio of average force and weight of potato
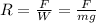 and since F=1235.06, m=0.500kg and g=9.8
and since F=1235.06, m=0.500kg and g=9.8
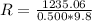 =252.05
=252.05
Therefore, ratio of average force to weight is 252.05