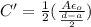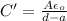Answer:
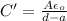
Solution:
As per the question:
Area of the plates is given by 'A'
Separation distance between the plates is 'd'
Now, after insertion of the metal plate with same area 'A' and thickness, a < d
in between the plates, the capacitance of the capacitor changes.
The capacitance of the air capacitor (parallel plate) is generally given by:
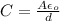
where
C = Capacitor's capacitance
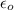 = Permittivity of the free space
= Permittivity of the free space
Now, when the metal slab is inserted the distance is reduced to (d - a)
Thus