Question

Assume that sample mean x overbar and sample standard deviation s remain exactly the same as those you just calculated but that are based on a sample of nequals25 observations. Repeat part a. What is the effect of increasing the sample size on the width of the confidence​ intervals?

Answer 1

As we increase the number of observations the width of the confidence interval decreases.

Explanation:

The general formula for the confidence interval for the mean is:

`IC[\mu, (1 - \alpha)\%] = \overline{x} \pm k\sqrt{Var(\overline{x})}`

And we know that the variance of
`\overline{x}` is:

`Var(\overline{x}) = Var((1)/(n) \sum_(i) x_i) = (1)/(n^2) Var(\sum_(i) x_i)`

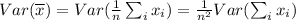
As it was informed the mean and the standard deviation remains the same during the process, so the second term
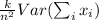`(k)/(n^2) Var(\sum_(i) x_i)` depends only on the number of observations, and the relationship is inverse. So if we increase the n the second term becomes smaller, and so the width of the interval decreases.