Question

This extreme value problem has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint. f(x, y, z) = 8x + 8y + 4z; 4x2 + 4y2 + 4z2 = 36 maximum value minimum value

Answer 1

Maximum value of f(x,y,z)=36 at (2,2,1)

Minimum value of f(x,y,z)=-36 at (-2,-2,-1)

Explanation:

We are given that

`f(x,y,z)=8x+8y+4z`

`g(x,y,z)=4x^2+4y^2+4z^2=36`

We have to find the extreme values of the function using Lagrange multipliers.

`f_x(x,y,z)=8`

`f_y(x,y,z)=8`

`f_z(x,y,z)=4`

`g_x(x,y,z)=8x`

`g_y(x,y,z)=8y`

`g_z(x,y,z)=8z`

`f_x=\lambda g_x`

`8=8x\lambda`

`x=(1)/(\lambda)`

`f_y=\lambda g_y`

`8=8y\lambda`

`y=(1)/(\lambda)`

`f_z=\lambda g_y`

`4=8z\lambda`

`z=(1)/(2\lambda)`

Substitute the values in g(x,y,z)

`4((1)/(\lambda))^2+4((1)/(\lambda))^2+4((1)/(2\lambda))^2=36`

`(4)/(\lambda^2)+(4)/(\lambda^2)+(1)/(\lambda^2)=36`

`(9)/(\lambda^2)=36`

`\lambda^2=(9)/(36)=(1)/(4)`

`\lambda=\pm(1)/(2)`

Substitute
`\lambda=(1)/(2)`

`x=2,y=2,z=1`

Substitute
`\lambda=-(1)/(2)`

`x=-2,y=-2,z=-1`

Now,
`f(2,2,1)=8(2)+8(2)+4(1)=16+16+4=36`

`f(-2,-2,-1)=8(-2)+8(-2)+4(-1)=-16-16-4=-36`

Maximum value of f(x,y,z)=36 at (2,2,1)

Minimum value of f(x,y,z)=-36 at (-2,-2,-1)

Answer 2

The maximum value= 36

Minimum value = - 36

Explanation:

Given that

f(x, y, z) = 8 x + 8 y + 4 z

h(x,y,z)=4 x² + 4 y² + 4 z² - 36

From Lagrange multipliers

Δf = λ Δh

Δf = < 8 ,8 , 4>

Δh = < 8 x ,8 y , 8 z>

Δf = λ Δh

So

< 8 ,8 , 4> = < 8 λ x ,8 λ y , 8 λ z>

8 = 8 λ x -------------1

8 = 8 λ y ---- ------2

4 = 8 λ z ----------------3

From equation 1 ,2 and 3

Now by putting the value of x,y and z in the following equation

4 x² + 4 y² + 4 z² = 36

`4* (1)/(\lambda^2 )+4* (1)/(\lambda^2 )+4* (1)/((2\lambda)^2 )=36`

`(4)/(\lambda^2 )+ (4)/(\lambda^2 )+ (1)/(\lambda^2 )=36`

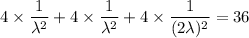
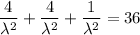
So the value of λ is

`\lambda =\pm (1)/(2)`

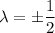
When λ = 1/2

x = 1 / λ , y=1 / λ , z= 1 /2 λ

x= 2 , y = 2 , z=1

So

f(x, y, z) = 8 x + 8 y + 4 z

f(2, 2, 1) = 8 x 2 + 8 x 2 + 4 x 1

f(2, 2, 1) =36

When λ = - 1/2

x = 1 / λ , y=1 / λ , z= 1 /2 λ

x= - 2 , y = - 2 , z= - 1

So

f(x, y, z) = 8 x + 8 y + 4 z

f(-2, -2, -1) = 8 x (-2) + 8 x (-2) + 4 x (-1)

f(-2, -2, -1) = - 36

The maximum value= 36

Minimum value = - 36