Answer:
The probability is 0.0428
Explanation:
First, let's remember that the binomial distribution is given by the formula:
![P(X=k) =\left[\begin{array}{ccc}n\\k\end{array}\right] p^(k)(1-p)^(n-k)](https://img.qammunity.org/2020/formulas/mathematics/college/adpowm2kqguv4b2y4trxz0sotf94rjp2kj.png) where k is the number of successes in n trials and p is the probability of success.
where k is the number of successes in n trials and p is the probability of success.
However, the problem tells us that when there isn't a number of trials fixed, we can use the geometric distribution and the formula for getting the first success on the xth trial becomes:
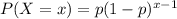
The problem asks us to find the probability of the first success on the 4th trial (given that the first subject to be a universal blood donor will be the fourth person selected)
Using this formula with the parameters given, we have:
p = 0.05
x = 4
Substituting these parameters in the formula and solving it, we get:

Therefore, the probability that the first subject to be a universal blood donor is the fourth person selected is 0.0428 or 4.28%