Question

Suppose you have three monodisperse polymer samples, A, B, and C, with molar masses of 100,000 g/mol, 200,000 g/mol, and 300,000 g/mol, respectively. Calculate the number average and weight-average molar mass of a blend obtained by mixing A, B, and C as follows: a) in equal proportions by weight b) in the molar ratio 1:1:1

Answer 1

a) Number-average molar mass: 163,700g/mol

Weight-average molar mass: 200,000g/mol

b) Number-average molar mass: 200,000g/mol

Weight-average molar mass: 233,300g/mol

Step-by-step explanation:

The number-average molar mass is based on mole% and weight-average molar mass is based on weight%, thus:

a) In equal proportions by weight:

number-average molar mass:

1g A×
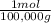`(1mol)/(100,000g)` = 1x10⁻⁵ moles A

1g B×
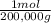`(1mol)/(200,000g)` = 5x10⁻⁶ moles B

1g C×
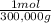`(1mol)/(300,000g)` = 3,33x10⁻⁶ moles C

Total moles are:

1x10⁻⁵ A + 5x10⁻⁶ B + 3,33x10⁻⁶ C = 1,833x10⁻⁵ moles.

Percent A:
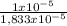`(1x10^(-5))/(1,833x10^(-5))`×100 = 54,5%

Percent B:
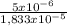`(5x10^(-6))/(1,833x10^(-5))`×100 = 27,3%

Percent C:
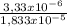`(3,33x10^(-6))/(1,833x10^(-5))`×100 = 18,2%

number-average molar mass:

0,545*100,000g/mol + 0,273*200,000g/mol + 0,182*300,000g/mol = 163,700g/mol

weight-average molar mass:

0,333*100,000g/mol + 0,333*200,000g/mol + 0,333*300,000g/mol = 200,000g/mol

b) In molar ratio 1:1:1

weight-average molar mass:

1mol A×
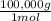`(100,000g)/(1mol)` = 100,000g A

1mol B×
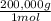`(200,000g)/(1mol)` = 200,000g B

1mol C×
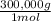`(300,000g)/(1mol)` = 300,000g C

Total mass is:

100,000 A + 200,000 B + 300,000 C = 600,000 g.

Percent A:
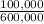`(100,000)/(600,000)`×100 = 16,7%

Percent B:
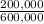`(200,000)/(600,000)`×100 = 33,3%

Percent C:
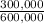`(300,000)/(600,000)`×100 = 50,0%

Weight-average molar mass:

0,167*100,000g/mol + 0,333*200,000g/mol + 0,500*300,000g/mol = 233,300g/mol

number-average molar mass:

0,333*100,000g/mol + 0,333*200,000g/mol + 0,333*300,000g/mol = 200,000g/mol

I hope it helps!