Question

Jim has an annual income of $180,000. Jim is looking to buy a house with monthly property taxes of $140 and monthly homeowners insurance of $70. Jim has $178 in monthly student loan payments. Apple bank has a maximum front end DTI limit of 28% and a maximum back end DTI limit of 36%. Both limits must be satisfied. Apple bank is offering a fully amortizing 30 year FRM at an annual rate of 4.5%, with monthly payments, compounded monthly. What is the biggest loan Jim can get?

Answer 1

$787,471.02

Step-by-step explanation:

Given:

Jim's annual income = $180,000

Monthly property taxes = $140

Monthly homeowners insurance = $70

Monthly student loan payments = $178

Maximum front end DTI limit = 28%

Maximum back end DTI limit = 36%

Amortizing period = 30 years = 360 months

annual rate = 4.5% compounded monthly

Now,

Monthly salary =
`\frac{\textup{Annual income}}{\textup{12 months}}`

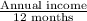
or

Monthly salary =
`\frac{\textup{180,000}}{\textup{12 months}}`

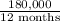
or

Monthly salary = $15,000

Maximum front end DTI limit

= (Maximum Monthly loan payment + monthly property taxes + monthly homeowner's insurance) ÷ Monthly income

0.28 × $15,000 = Maximum Monthly loan payment + $140 + $70

Maximum Monthly loan payment = $4,200 - $140 - $70

= $3,990

and,

Maximum back end DTI limit =

or

0.36 × $15,000 = Maximum Monthly loan payment + $140 + $70 + $178

or

Maximum Monthly loan payment = $5,400 - $140 - $70 - $178

= $5,012

Now,

The monthly payment = minimum of [ $3990, $5012 ]

therefore,

The monthly payment = $3,990

Thus,

The maximum amount of loan = Monthly payment ×
`[((1-(1+(r)/(k))^(-kn)))/(((r)/(k)))]`

here,

k = 12 when compounded monthly

n = 30 years

r = 4.5% = 0.045

The maximum amount of loan = $3,990 ×
`[((1-(1+(0.045)/(12))^(-12*30)))/(((0.045)/(12)))]`

or

The maximum amount of loan = $787,471.02