Question

A force of 1600 N acts parallel to a ramp to push a 300-kg piano into a moving van. The ramp is inclined at 20° . (a) What is the acceleration of the piano up the ramp? (b) What is the velocity of the piano when it reaches the top if the ramp is 4.0 m long and the piano starts from rest

Answer 1

(a) a = 1.98 m/s2

(b) v = 3.98 m/s

Step-by-step explanation:

(a) For this first part, we should set the "x" axis along the ramp and then decompose the weight of the piano, the corresponding weight acting along our "x" axis will be equal to the total weight multiplied by the sine of the inclination angle:

`W'= W* sin(20)\\W'=300*9.8*sin(20) = 1005.54 N`

This force acts in the opposite direction to the force applied to push the piano.

According to Newton's second law, the net force acting on a body is given by its mass times acceleration, therefore:

`F=m*a\\1600 - 1005.54 = 300*a\\a=1.98m/s^(2)`

(b) The displacement of the piano is 4m. According to Torricelli's Equation, its velocity can be found as follows:

`v_(f) ^(2)=v_(i) ^(2) +2*a*x'\\v_(f) ^(2)=0 ^(2) +2*1.98*4\\v_(f)= 3.98m/s`

Answer 2

(a) The acceleration is 1.98 m/s²

(b) The velocity of the piano is 3.98 i m/s

Step-by-step explanation:

In order to answer part (a) you have to apply Newton's Second Law which is:

∑F=mA

where F is all the forces, m is the mass and A is the acceleration.

You have to perfom a Free Body Diagram for the piano (see the attachment)

Applying Newton's Second Law:

x-axis: F - mgSin(20°) =mA

Notice that mgSin(20°) is the x component of the weight

Replacing the given values:

1600 - (300)(9.8)Sin(20°) = 300A

594.5 = 300A

Dividing by 300 both sides:

A=594.5/300

A=1.98 m/s²

For part (b) you have to apply the Work-Energy Theorem which is:

Work of all non-conservative forces = ΔEm

where ΔEm is the variation of mechanical energy in two points a and b

The work is represented by:

W=
`\int\limits^b_a {F o ds} \,`

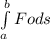
Notice that the only force producing work is the force of 1600 N because is the only non-conservative force in the direction of the displacement.

In this case, ds: dx i

F= 1600 i

a= 0 m and b =4.0 m

So, you have to calculate the dot product between vectors F and ds which is:

|F||ds|Cos(0°)=1600dx

The angle between them is 0° because they are parallels and in the same direction.

Calculating the work:

W=
`\int\limits^4_0 {1600} \, dx=1600x` evaluated in x=0 and x=4

W=1600(4)-1600(0)=6400 J

Now, ΔEm=ΔEk+ΔEp

where ΔEk is the variation of kinetic enery and ΔEp is the variation of potential energy

In this case ΔEp=mgh, where h is the height of the ramp (4Sin20)

ΔEk between a and b = Ekb-Eka

Ekb-Eka=6400

Eka=0 because the piano starts from rest (Va=0)

Ekb=6400

`(1)/(2)mVb^(2) + mgh=6400`

`(300)/(2)Vb^(2) +(300)(9.8)(4)Sin(20)=6400`

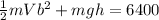
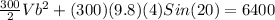
Solving for Vb:

Vb= 3.98 m/s

So, the velocity vector is:

Vb= 3.98 i m/s