Question

1. Solve the rational equation quantity 4 times x plus 3 end quantity divided by 5 equals quantity 8 times x minus 1 end quantity divided by 9.

x = 0.5

x = 2

x = 8

x = 9

2. Determine the vertical asymptote for the rational function f of x equals quantity x minus 4 end quantity divided by quantity 2 times x plus 3 end quantity.

x = −4
x equals negative three halves
x equals three halves
x = 4

Answer 1

1. x = 8

2.
`x=-(3)/(2)`

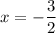
Explanation:

1. Solve the rational equation

`(4x+3)/(5)=(8x-1)/(9)`

First, cross multiply:

`9(4x+3)=5(8x-1)`

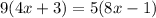
Now, use distributive property:

`36x+27=40x-5`

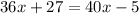
Separate terms with x and without x into different sides of equation:

`36x-40x=-5-27`

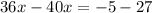
Simplify:

`-4x=-32`

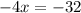
Divide by -4:

`x=8`

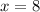
2. The rational function

`f(x)=(x-4)/(2x+3)`

This rational function is undefined for all values of x, for which the denominator is equal to 0. Find these values:

`2x+3=0\\ \\2x=-3\\ \\x=-(3)/(2)`

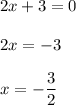
This means that the line
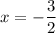`x=-(3)/(2)` is a vertical asymptote for the rational function f(x).