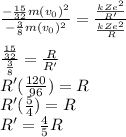Question

A proton is projected toward a fixed nucleus of charge +Ze with velocity vo. Initially the two particles are very far apart. When the proton is a distance R from the nucleus its velocity has decreased to 1/2 vo. How far from the nucleus will the proton be when its velocity has dropped to 1/4 vo?

Answer 1

`(4)/(5)R`

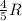
Step-by-step explanation:

Using the law of conservation of energy for both cases, when the proton is at distance R from the nucleus with a final velocity equal to
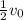`(1)/(2)v_0` and when the proton is at distance R' from the nucleus with a final velocity equal to
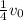`(1)/(4)v_0`. Recall that initially the two particles are very far apart, so there is no initial potential energy. For the first case, we have:

`\Delta K=\Delta U\\K_(f)-K_(i)=U_(f)-U_(i)\\(1)/(2)m(v_(f))^2-(1)/(2)m(v_(0))^2=(ke(Ze))/(R)-0\\(1)/(2)m((1)/(2)v_(0))^2-(1)/(2)m(v_(0))^2=(kZe^2)/(R)\\(1)/(2)m(1)/(4)(v_(0))^2-(1)/(2)m(v_(0))^2=(kZe^2)/(R')\\(1)/(8)m(v_(0))^2-(1)/(2)m(v_(0))^2=(kZe^2)/(R')\\-(3)/(8)m(v_(0))^2=(kZe^2)/(R)(1)\\`

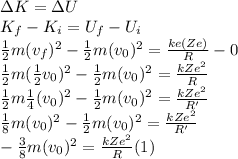
In the same way, for the second case, we have:

`(1)/(2)m((1)/(4)v_(0))^2-(1)/(2)m(v_(0))^2=(ke(Ze))/(R')\\(1)/(2)m(1)/(16)(v_(0))^2-(1)/(2)m(v_(0))^2=(kZe^2)/(R')\\(1)/(32)m(v_(0))^2-(1)/(2)m(v_(0))^2=(kZe^2)/(R')\\-(15)/(32)m(v_(0))^2=(kZe^2)/(R')(2)\\`

Finally, dividing (2) in (1):

`(-(15)/(32)m(v_(0))^2)/(-(3)/(8)m(v_(0))^2)=((kZe^2)/(R'))/((kZe^2)/(R))\\\\((15)/(32))/((3)/(8))=(R)/(R')\\R'((120)/(96))=R\\R'((5)/(4))=R\\R'=(4)/(5)R`