Question

Determine p if the following equation has equal roots: (p-3)xsquare + 4(p-3)x + 4 = 0

Answer 1

A quadratic equation
`ax^2+bx+c=0` has equal roots if and only if the determinant

`\Delta = b^2-4ac`

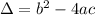
equals zero.

In this case,

`a=p-3,\quad b=4(p-3),\quad c=4`

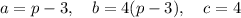
So, the determinant is

`[4(p-3)]^2-4\cdot (p-3)\cdot 4`

Expand the square and multiply terms to get

`[4(p-3)]^2-4\cdot (p-3)\cdot 4=16(p-3)^2-16(p-3) = 16(p-3)[(p-3)-1)`

Which finally simplifies to

`16(p-3)(p-4)`

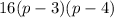
This expression equals zero if one of the factors equals zero:

`p-3=0 \iff p=3,\quad p-4=0 \iff p=4`