Question

The midpoint of AB is M(-5,1). If the coordinates of A are (-4,-5), what are the coordinates of B?

Answer 1

The midpoint of AB is M(-5,1). The coordinates of B are (-6, 7)

SOLUTION:

Given, the midpoint of AB is M(-5,1).

The coordinates of A are (-4,-5),

We need to find the coordinates of B.

We know that, mid-point formula for two points A
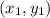`(x_(1), y_(1))` and B
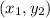`(x_(1), y_(2))` is given by

`M\left(x_(3), y_(3)\right)=\left((x_(1)+x_(2))/(2), (y_(1)+y_(2))/(2)\right)`

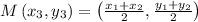
Here, in our problem,
`\mathrm{x}_(3)=-5, \mathrm{y}_(3)=1, \mathrm{x}_(1)=-4 \text { and } \mathrm{y}_(1)=-5`

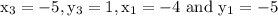
Now, on substituting values in midpoint formula, we get

`(-5,1)=\left((-4+x_(2))/(2), (-5+y_(2))/(2)\right)`

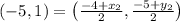
On comparing, with the formula,

`(-4+x_(2))/(2)=-5 \text { and } (-5+y_(2))/(2)=1`

`-4+\mathrm{x}_(2)=-10 \text { and }-5+\mathrm{y}_(2)=2`

`\mathrm{x}_(2)=-6 \text { and } \mathrm{y}_(2)=7`

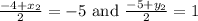
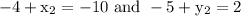
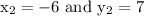
Hence, the coordinates of b are (-6, 7).