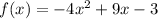Question

Find the quadratic function passing through the points (0,-3), (1,2), and (2,-1)

Answer 1

The quadratic function passing through the points (0,-3), (1,2), and (2,-1) is
`\mathrm{f}(\mathrm{x})=-4 x^(2)+9 x-3`

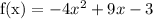
Solution:

Given that required function is quadratic

And function is passing through points (0 , -3) , (1 , 2) and (2 , -1)

General form of a quadratic function is
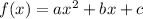`f(x)=a x^(2)+b x+c` ----(A)

f(x) is nothing but output value that is y.

That is f(x) = y

So
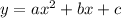`y=a x^(2)+b x+c` --- (1)

Let’s use equation (1) to get required function.

Given that function passes through (0 , -3) means when x = 0 , y = -3

On substituting value of x and y in equation (1) we get

`-3=\mathrm{a}(0)^(2)+\mathrm{b}(0)+\mathrm{c}`

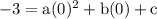
-3 = 0 + 0 + c

c = -3

On substituting value of c in equation (1) we get

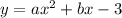`y=a x^(2)+b x-3` ---(2)

Function also passes through point (1, 2) that is at x = 1 , y = 2.

On substituting value of x and y in equation (2) we get

`2=\mathrm{a}(1)^(2)+\mathrm{b}(1)-3`

2 = a + b – 3

a + b = 5

b = 5 - a -------(3)

Also given function passes through point ( 2 , -1) means when x = 2 , y = -1

On substituting value of x and y in equation (2) we get

`-1=\mathrm{a}(2)^(2)+\mathrm{b}(2)-3`

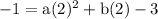
-1 = 4a + 2b – 3

4a + 2b = 2

2a + b = 1 ------- (4)

On substituting value of b from equation (3) in equation (4), we get

2a + (5 - a ) = 1

a + 5 = 1

a = 1-5 = -4

From equation (3) b = 5 – a = 5 – (-4) = 9

b = 9

Now we have a = -4, b = 9 and c = -3

On substituting calculated values of a, b, and c in equation (A) we get

`f(x)=-4 x^(2)+9 x-3`

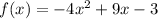
Hence required quadratic function is
`f(x)=-4 x^(2)+9 x-3`