Question

A new machine makes 20,000 aluminum cans three times faster than an older machine. With both machines operating, it takes 15 h to make 20,000 cans. How long would it take the new machine, working alone, to make 20,000 cans?

Answer 1

To find the time it takes for the new machine to make 20,000 cans, we first need to determine how long it takes for the old machine to make 20,000 cans. Since the new machine makes cans three times faster than the old machine, the new machine can make 20,000 cans in 5 hours.

Step-by-step explanation:

To find the time it takes for the new machine to make 20,000 cans, we first need to determine how long it takes for the old machine to make 20,000 cans. Since both machines together can make 20,000 cans in 15 hours, we can determine the rate at which they work together by dividing the number of cans by the time: 20,000 / 15 = 1,333.33 cans per hour.

Since the new machine makes cans three times faster than the old machine, we can multiply the rate of the old machine by 3 to find the rate of the new machine: 1,333.33 * 3 = 3,999.99 cans per hour.

Finally, we can find the time it takes for the new machine to make 20,000 cans by dividing the number of cans by the rate: 20,000 / 3,999.99 = 5 hours (rounded to the nearest whole hour).

Answer 2

New machine, working alone will take 20 hours to complete 20000 aluminium cans.

Solution:

For sake of simplicity let’s assume new machine be Machine “N” and old machine be Machine “O”

Let’s assume cans manufacture by machine “O” in 1 hour = x

Since machine N is three times faster than “O”,

So cans manufacture by machine N in 1 hour = 3x

Cans manufactured in 1 hour when both machines are operating simultaneously is equal to cans manufacture by machine O in 1 hour + cans manufacture by machine N in 1 hour

That is cans manufactured in 1 hour when both machines are operating = x + 3x = 4x

So cans manufactured in 15 hours when both machines are operating =
`15 * 4x = 60x`

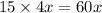
Given that cans manufactured in 15 hours when both machines are operating = 20000

60x = 20000

`3x * 20 = 20000`

`3x = (20000)/(20)`

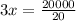
3x = 1000 cans

As cans manufacture by machine N in 1 hour = 3x = 1000

So number of hours required by machine N to produce 1000 cans alone = 1 hour

So number of hours required by machine N to produce 1 can alone =
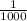`(1)/(1000)` hours

And number of hours required by machine N to produce 20000 cans =
`20000 * (1)/(1000)` = 20 hours

Hence new machine, working alone will take 20 hours to complete 20000 cans.