Answer:
The probability is
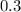
Explanation:
Let's start defining the random variable.
X : '' Voltage levels ''
We know that X has an uniform distribution ⇒
X ~ U [ a , b ]
Where ''a'' and ''b'' define the interval.
In this exercise, X ~ U [ 123.0 , 125.0 ] (We can notice this in the graph of the density function).
The density function for an uniform distribution is
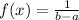 when x ∈ [ a , b ] and
when x ∈ [ a , b ] and
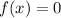 otherwise.
otherwise.
In this exercise :
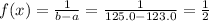
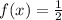 when x ∈ [ 123.0 , 125.0 ]
when x ∈ [ 123.0 , 125.0 ]
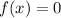 otherwise
otherwise
To find the probability
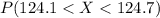 we need to integrate the function
we need to integrate the function
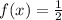 between 124.1 and 124.7
between 124.1 and 124.7
This integrate is equal to the area below the graph of the function between 124.1 and 124.7
Given that the graph is a rectangle with height 0.5 :
This area is

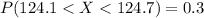
And that is the probability we need. We could have done the integral but it was not necessarily.