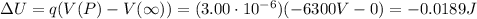(a) -6300 V
To find the total potential at point P, we can just sum the potential due to the charge q1 and the potential due to the charge q2.
The formula for the potential is:
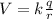
where
k is the Coulomb's constant
q is the charge
r is the distance from the charge
For charge q1,
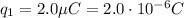
r = 4.0 m
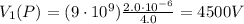
For charge q2,
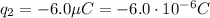
while the distance is:
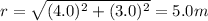
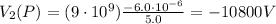
So, the total potential at P is
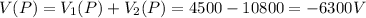
(b) -0.0189 J
The change in potential energy of a charge moving in an electric field is
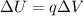 (1)
(1)
where
q is the charge
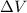 is the potential difference
is the potential difference
Here the charge starts from infinity, where the potential is
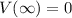
And the charge is
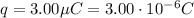
And solving for eq.(1), we find