Question

What is the value of C in the matrix equation below?

Answer 1

4, 2, -7

Explanation:

-18 - 4= -22

3 - 2= 1

5 (-)-7= 12

+

Answer 2

C.
`C=\begin{bmatrix}4&2& -7\end{bmatrix}`

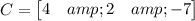
Explanation:

We are given that an equation

`\begin{bmatrix}-18&3&5\end{bmatrix}-C=\begin{bmatrix}-22&1&12\end{bmatrix}`

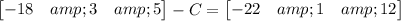
We have to find the value of C.

Let C=
`\begin{bmatrix}a&b& c\end{bmatrix}`

`\begin{bmatrix}-18&3&5\end{bmatrix}-\begin{bmatrix}a&b& c\end{bmatrix}=\begin{bmatrix}-22&1&12\end{bmatrix}`

`\begin{bmatrix}-18-a&3-b& 5-c\end{bmatrix}=\begin{bmatrix}-22&1& 12\end{bmatrix}`

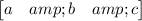
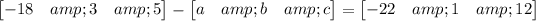
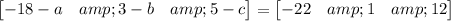
When two matrix are equal then each element equals to its corresponding element.

Therefore, -18-a=-22

`a=-18+22=4`

`3-b=1`

`b=3-1=2`

`5-c=12`

`c=5-12=-7`

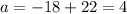
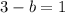
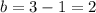
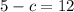
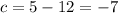
Substitute the values then we get

`C=\begin{bmatrix}4&2& -7\end{bmatrix}`

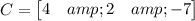
Hence, option C is true.