Question

Determine whether the function f(x) = 3x4 is even or odd.

a. The function is even because f(x) = f(−x).
b. The function is odd because f(x) = f(−x).
c. The function is even because −f(x) = f(x).
d. The function is odd because −f(x) = f(x).

Answer 1

The function
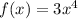`f(x) = 3x^4` is an even function because it satisfies the condition f(x) = f(-x), which means it is symmetric about the y-axis.

Step-by-step explanation:

The student has asked to determine whether the function
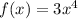`f(x) = 3x^4` is even or odd. To establish whether a function is even or odd, we can use the definitions: an even function satisfies f(x) = f(-x), implying symmetric behavior about the y-axis, while an odd function satisfies -f(x) = f(-x), implying symmetry with respect to the origin where the function is reflected along both axes.

For the given function, let's verify the behavior for negative inputs:

`f(x) = 3x^4`

`f(-x) = 3(-x)^4 = 3x^4`

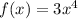
Since f(-x) is equal to f(x), by the definition of an even function, we conclude that the function
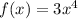`f(x) = 3x^4` is even.

Therefore, the correct answer is option (a): The function is even because f(x) = f(-x).