Question

A major corporation is building a 4325-acre complex of homes, offices, stores, schools, and churches in the rural community of Glen Cove. As a result of this development, the planners have estimated that Glen Cove's population (in thousands) t years from now will be given by(25t2 + 150t + 100)/(t2 + 6t + 24)(a) Find the rate at which Glen Cove's population is changing with respect to time.(b) What will be the population after 10 years? (Round your answer to the nearest person.)(c)At what rate will the population be increasing when t = 10? (Round your answer to the nearest integer.)

Answer 1

a) The rate at which the population is changing with respect to time is

`P'(t)=(1000t+3000)/((t^2+6t+24)^2)`

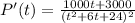
b) The population after 10 years will be 22 283 people.

c) The rate at the population will be increasing when t = 10 is 38 persons per year.

Explanation:

a) The rate of change can be found with the derivative of P(t).

to solve this you have to consider the rule to derivate a cocient:

`F'=(u'v-uv')/(v^2)`

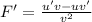
In this case:

`u=25t^2+150t+100\\v=t^2+6t+24\\u'=50t+150\\v'=2t+6`

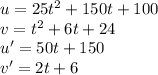
Replacing the values and simplifing the equation you can find:

`F'(t)=((50t+150)(t^2+6t+24)+(25t^2+150t+100)(2t+6))/((t^2+6t+24)^2)`

`F'(t)=(1000t+3000)/((t^2+6t+24)^2)`

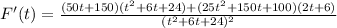
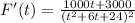
b) The population after 10 years can be found by solving P(t) for t=10:

`P(t=10)(25(10)^2+150(10)+100)/((10)^2+6(10)+24)=(1025)/(46)=22.22826`

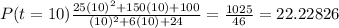
and if you round your answer to the nearest person the population will be 22 283 people.

c) The rate at the population will be increasing when t=10 can be found solving P'(t) for t=10:

`P'(t)=(1000(10)+3000)/(((10)^2+6(10)+24)^2)=(1625)/(4232)=0.3839`

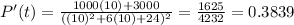
and if you round your answer to the nearest integer you find that the answer is 38 person per year.