Question

A furniture shop refinishes chairs. Employees use one of two methods to refinish each chair. Method I takes 0.5 hours and the material costs $9. Method II takes 2.5 hours, and the material costs $7. Next week, they plan to spend 199 hours in labor and $1226 in material for refinishing chairs. How many chairs should they plan to refinish with each method?

Answer 1

method I = 88 chairs

method II = 62 chairs

Step-by-step explanation:

This problem can be modeled by a system of two linear equations.

Define x as the number of chairs refinished by method I and y by method II

The sum of hours spent on both methods should equal 199 and the sum of total material cost should equal $1226, therefore:

`0.5x + 2.5y = 199`

`9x+7y = 1226`

Multiplying the first equation by -18 and adding it to the second equation we can solve for the value of y:

`9x+7y +(-9x - 45)= 1226+(-3582)\\y=(2356)/(38) = 62\\`

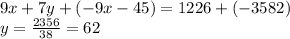
We can now apply the value of y found to the first equation and solve for x:

`0.5x+2.5*62 = 199\\x=(199 - (2.5*62))/(0.5) = 88`

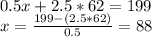
Therefore, they should refinish 88 chairs with method I and 62 chairs with method II