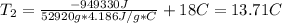Question

A certain commercial process relies on the addition of NH4NO3 to a solution of their proprietary compound. The Junior Apprentice Chemist develops a plan to add 6.55 pounds of NH4NO3 to 14.0 gallons of water. The water in the factory is typically at an initial temperature of 18.0 C, and the temperature of the water cannot drop below 15 C, or the reaction will be too slow. Will the above plan work? Use the value of Delta Hrxn = +25.7 kJ/mol.

Answer 1

Final temperature 13.71 C the plan won't work

Step-by-step explanation:

Reaction:

`NH_(4)NO_(3) + H_(2)O - -> HNO_(3) + NH_(4)OH       H_(rxn)=+25.7(kJ)/(mol){`

Mol of
`NH_(4)NO_(3)`

`6.55 Lb*(453.59g)/(1Lb)*(1mol)/(80.43g)=36.93 mol`

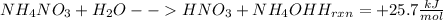
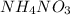
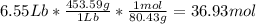
Mol of water

`14 gallons*(3.78L)/(1 gallon)*(1000 g)/(1L)*(1 mol)/(18 g)=2940 mol`

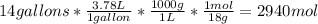
The reaction stoichiometry is 1:1 so the
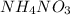`NH_(4)NO_(3)` with 36.93 mol is the limit reagent in the reaction.

The energy for this reaction is:

`Q=H_(rxn)*mol-of- NH_(4)NO_(3)= +25.7(kJ)/(mol)*36.93 mol=949.33kJ`

The process is getting this energy from the water for that reason the temperature of the water will decrease.

Q necessary for the reaction is

[
`Q=m_{NH_(4)NO_(3)}*Cp_ {NH_(4)NO_(3)}*(T_(2)-T_(1))`

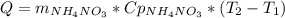
The heat given by the water will be the same but with a different sign

[
`-Q=m_{H_(2)O} Cp_ {H_(2)O}*(T_(2)-T_(1))`

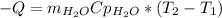
We estimate the water’s final temperature, with this equation:

Clearing for T2 we get:

`T_(2)=\frac{-Q}{m_{H_(2)O}*Cp_ {H_(2)O}}+T_(1)`

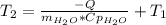
mass of water =52920g

Cp=4.186 J/g*C

`T_(2)=(-949330J)/(52920g*4.186J/g*C)+18 C= 13.71 C`